Question

A laser pulse of duration 25 ms has a total energy of 1.4 J. The wavelength of this radiation is

567 nm. How many photons are emitted in one pulse? Let 1 eV = 1.60 x 10-19 J, the mass of
an electron m=9.11 10-31
kg, the speed of light c= 3.00 x 108 m/s, and Planck's constant h
= 4.136 10-15 eV .s.

Answer 1

n = 4 x 10¹⁸ photons

Step-by-step explanation:

First, we will calculate the energy of one photon in the radiation:

`E = (hc)/(\lambda)\\\\`

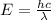
where,

E = Energy of one photon = ?

h = Plank's Constant = 6.625 x 10⁻³⁴ J.s

c = speed of light = 3 x 10⁸ m/s

λ = wavelength of radiation = 567 nm = 5.67 x 10⁻⁷ m

Therefore,

`E = ((6.625\ x\ 10^(-34)\ J.s)(3\ x\ 10^8\ m/s))/(5.67\ x\ 10^(-7)\ m)`

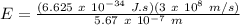
E = 3.505 x 10⁻¹⁹ J

Now, the number of photons to make up the total energy can be calculated as follows:

`Total\ Energy = nE\\1.4\ J = n(3.505\ x\ 10^(-19)\ J)\\n = (1.4\ J)/(3.505\ x\ 10^(-19)\ J)\\`

n = 4 x 10¹⁸ photons