Question

Evaluate the indicated limit algebraically. Change the form of the function where necessary. Please write clearly with description of each step, thank you very much.

3x^2+4.5
________
x^2-1.5

lim
x → ∞

Answer 1

`\displaystyle \lim_(x\to \infty)(3x^2+4.5)/(x^2-1.5)=3`

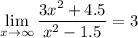
Explanation:

We want to evaluate the limit:

`\displaystyle \lim_(x\to \infty)(3x^2+4.5)/(x^2-1.5)`

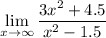
To do so, we can divide everything by x². So:

`=\displaystyle \lim_(x\to \infty)(3+4.5/x^2)/(1-1.5/x^2)`

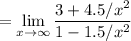
Now, we can apply direct substitution:

`\Rightarrow \displaystyle (3+4.5/(\infty)^2)/(1-1.5/(\infty)^2)`

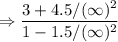
Any constant value over infinity tends towards 0. Therefore:

`\displaystyle =(3+0)/(1+0)=(3)/(1)=3`

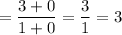
Hence:

`\displaystyle \lim_(x\to \infty)(3x^2+4.5)/(x^2-1.5)=3`

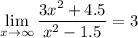
Alternatively, we can simply consider the biggest term of the numerator and the denominator. The term with the strongest influence in the numerator is 3x², and in the denominator it is x². So:

`\displaystyle \Rightarrow \lim_(x\to\infty)(3x^2)/(x^2)`

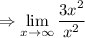
Simplify:

`\displaystyle =\lim_(x\to\infty)3=3`

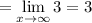
The limit of a constant is simply the constant.

We acquire the same answer.