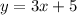Answer:
y = 3x + 5
Explanation:
1) First, find the slope between the pair of points. Use the slope formula
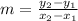 . Substitute the x and y values of points A and B into the formula and simplify:
. Substitute the x and y values of points A and B into the formula and simplify:
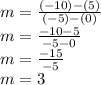
So, the slope is 3.
2) Now, identify the y-intercept of the line, or the point at which the line intersects the y-axis. All points on the y-axis have an x-value of 0. We're told that (0,5) is a point the line intersects, and since it has an x-value of 0, that must be the y-intercept.
3) Using slope-intercept format, represented by the equation
 , write the equation of the line. Remember that the number in place of
, write the equation of the line. Remember that the number in place of
 , or the coefficient of the x-term, is the slope. So, substitute 3 for
, or the coefficient of the x-term, is the slope. So, substitute 3 for
 . Also, remember that
. Also, remember that
 represents the y-intercept of a line, so substitute 5 in its place, too. This gives the following answer:
represents the y-intercept of a line, so substitute 5 in its place, too. This gives the following answer: