Question

Martin is dilating a blue triangle to create a yellow triangle. If he used a scale factor of

Which statement is true?

Answer

A

B

The perimeter of the yellow triangle will be 12/25 times the perimeter of the blue triangle.

The perimeter of the yellow triangle will be times the perimeter of the blue triangle.

The area of the yellow triangle will be times the area of the blue triangle.

С

D

The area of the yellow triangle will be

4

25

times the area of the blue triangle.

Previous

Answer 1

See Explanation

Explanation:

The question has missing details, as the scale factor is not given. However, I will give a general explanation on how to calculate the area and perimeter of a dilated shape (triangle).

The following assumptions, apply:

(1) Scale factor of 1/2 from the blue to the yellow triangle.

(2) The dimension of the blue triangle are:

`Base = x`

`Sides= y\ and\ z`

`Height= h`

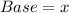
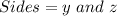
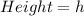
First, calculate the dimensions of the yellow triangle.

The dimension will be the product of the scale factor and the dimensions of the blue triangle.

So, we have:

`Base = (1)/(2) * x = (1)/(2)x`

`Sides = (1)/(2)y\ and\ (1)/(2)z`

`Height = (1)/(2)h`

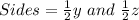
The perimeter of the blue triangle is:

`P_1 =Base + Sides`

`P_1 = x + y + z`

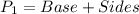
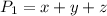
The perimeter of the yellow triangle is:

`P_2 =Base + Sides`

`P_2 = (1)/(2)x + (1)/(2)y + (1)/(2)z`

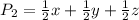
Factorize

`P_2 = (1)/(2)[x + y + z]`

Recall that:
`P_1 = x + y + z`

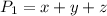
So:

`P_2 = (1)/(2)*P_1`

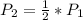
This implies that the perimeter of the yellow triangle is a product of the scale factor and the perimeter of the blue triangle.

The area of the blue triangle is:

`A_1 = (1)/(2)* Base * Height`

`A_1 = (1)/(2) * x* h`

`A_1 = (1)/(2) xh`

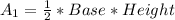
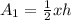
The area of the yellow triangle is:

`A_2 = (1)/(2) * Base * Height`

`A_2 = (1)/(2)* ((1)/(2)x) * ((1)/(2)h)`

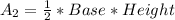
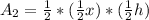
Rewrite as:

`A_2 = (1)/(2)* (1)/(2) [(1)/(2)x h]`

`A_2 = ((1)/(2))^2 *[(1)/(2)x h]`

Recall that:
`A_1 = (1)/(2) xh`

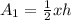
So:

`A_2 = ((1)/(2))^2 *A_1`

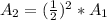
This implies that the area of the yellow triangle is a product of the square of the scale factor and the area of the blue triangle.