Question

Select the correct comparison set a set b O A the typical value is greater is set a the spread is greater in set b

Answer 1

(a)

Explanation:

Given

See attachment for sets A and B

Required

The true statement about both sets

First, we calculate the typical values (mean) of set A and set B.

This is calculated as:

`Mean = (\sum fx)/(\sum f)`

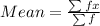
For A:

`A= (0*1+2*1+5*1+6*1+7*1)/(1+1+1+1+1)`

`A= (20)/(5)`

`A =4`

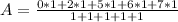
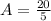
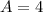
For B:

`B = (7 * 1 + 8 *1 + 9 * 2 + 10 * 1)/(1+1+2+1)`

`B = (43)/(5)`

`B = 8.6`

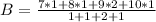
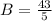
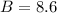
Here, we can conclude that B has a larger typical value

Next calculate the spread (range) of sets A and B

This is calculated as:

`Range = Highest -Least`

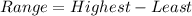
For A:

`A = 7 - 0`

`A = 7`

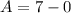
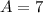
For B

`B=10 - 7`

`B = 3`

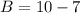
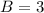
Here, we can conclude that A has a larger spread.

Hence, (a) is true