Basic Trigonometric Ratios
We can identify the sides of a right triangle by describing their location in relation to a given angle.
- The "hypotenuse" is the longest side of a right triangle. It is opposite the right angle.
- The "opposite" is the side that the angle does not touch.
- The "adjacent" is the side that the angle does touch, that is not the hypotenuse.
There are three basic trigonometric ratios:
- The sine ratio:
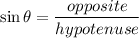
- The cosine ratio:
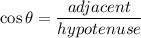
- The tangent ratio:
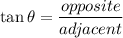
We use theta (θ) to represent an angle.
Solving the Question
We are asked to find
 in the triangle.
in the triangle.
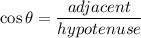
The side adjacent to β measures 8 units.
The hypotenuse of the right triangle measures 17 units.
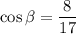
Answer
Therefore,
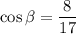 .
.