Question

How many different 3-digit odd number can be formed with the digit 0,1,2 up to 9 if the repitition of digits is not allowed

Answer 1

The answer is "320".

Explanation:

They have to be 1, 3, 5, 7, and 9 as your final digit. Your middle digit may be anything other than the first digit, and only the last digit or 0, is anything.

Now let us take a look at strange digits ending in 1.

This can start from any digit other than 0, so there are 8 options during the first digit.

Its middle digit could only be 1 digit and 1 digit. Even so, it can also be 0, since it has 8 options.

So,
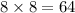`8* 8 = 64` strange number ending in 1.

For other strange amounts, the very same logic is working.

And thus there are 64 possible odd numbers for just about any number ending in any of the five odd digits: 1, 3, 5, 7, or 9.

The answer is
`5 * 64 = 320`.