Question

An effect analogous to two-slit interference can occur with sound waves, instead of light. In an open field, two speakers placed 1.19 m apart are powered by the same function generator producing sine waves at 1,163 Hz frequency. Assume that the speed of sound is 340 m/s. A student walks along a line 12.5 m away and parallel to the line from one speaker to the other speakers. She hears an alternating pattern of loud and quiet, due to constructive and destructive interference. What is the distance between the central maximum and the first maximum (loud) position along this line in m

Answer 1

3.04 m

Step-by-step explanation:

The interference by diffraction of waves is noticeable only when the dimension of the opening through which the wave is passing through is comparable to the wavelength of the passing wave.

It is given that :

Distance between two speakers, d = 1.19 m

Speed of sound, v = 340 m/s

The frequency is f = 1163 Hz

Distance the student walk along the line of the speaker, D = 12.5 m

We know the wavelength of the sound produced by the speakers is given by :

`$\lambda=(v)/(f)$`

`$=(340)/(1163)$`

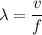
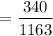
= 0.29 m

Now the distance between the central maximum and the first maximum position is given by :

`$y=(\lambda D)/(d)$`

`$=(0.29 * 12.5)/(1.19)$`

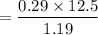
= 3.04 m