Question

Answer this ASAP : The company is also having a problem deciding on a torso design for Tinker. Each design has a height of 10 cm. Below are the three choices they have decided on. 3) Each of the torsos is filled with chocolate. One of the managers wants to throw out Design C. He argues that the amount of chocolate needed to fill it is so much more than the other two types that it shouldn't even be a choice. Is he right or wrong? Explain.​

Answer 1

All three designs will hold he same amount of chocolate (60 cubic centimeters). So, the manager is wrong.

Explanation:

Let's find the volume of each design.

For Design A, the cross section is a rectangle rectangle measured 3 cm by 2 cm.

Therefore, the area of the cross section is:

`A_1=3(2)=6\text{ cm}^2`

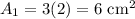
Since the height is 10 cm, the total volume of Design A is:

`V_1=10(6)=60\text{ cm}^2`

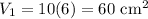
For Design B, the cross section is also a rectangle measuring 3 cm by 2 cm.

So, the area of the cross section is:

`A_2=3(2)=6\text{ cm}^2`

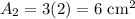
And the height is still 10 cm. So, the total volume of Design B is:

`V_2=6(10)=60\text{ cm}^3`

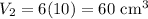
Note that we use the vertical height, and not the slant height. If this seems confusing, imagine each layer being a cracker. If 10 crackers were laid on top of each other perfectly, that is Design A. However, if we were to move each cracker to the right a bit, that is Design B. The volume of both cases are the same.

For Design C, the cross section is a triangle with a base length of 6 cm and a height of 2 cm.

So, the area of the cross section is:

`\displaystyle A_3=(1)/(2)(2)(6)=6`

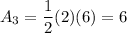
And since the height is 10 cm, the volume of Design C is:

`V_3=6(10)=60\text{ cm}^3`

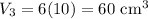
Therefore, as we can see, all three designs will hold he same amount of chocolate. So, the manager is wrong.