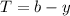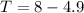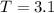Question

The bottom edge of a 16-foot long cantilever is given by the equation y = 2Vx, where y is the distance the

bottom edge is from ground height, in feet.

y

(a) What is the value of b, the height of the

cantilever, in feet?

b

T

y=2&x

b) To the nearest tenth of a foot, what is the

thickness, T, of the cantilever at x =6 feet?

Answer 1

`(a)\ b = 8`

`(b)\ T = 3.1`

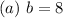
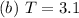
Explanation:

Given

`y = 2\sqrt x`

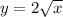
See attachment

Solving (a): Find b

At point b,
`x = 16`

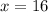
So, the value of b is:

`b = 2 * \sqrt{16`

`b = 2 * 4`

`b = 8`

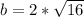
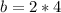
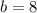
Solving (b): Find T

First, we calculate the value of y at point T

`y = 2\sqrt x`

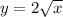
At point T,
`x = 6`

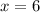
So:

`y = 2 * \sqrt 6`

`y = 2 * 2.45`

`y = 4.9`

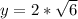
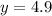
To calculate T, we subtract the calculated height (y) from the value of b

`T =b - y`

`T = 8 - 4.9`

`T = 3.1`