Given:
The base of an isosceles triangle is 16 cm long.
The equal sides are each 22 cm long.
To find:
The height of the triangle.
Solution:
We know that the altitude of an isosceles triangle divides the base into two equal parts as shown in the below figure.
According to the Pythagoras theorem:

Using Pythagoras theorem, we get
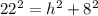
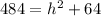
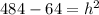
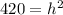
Taking square root on both sides, we get
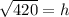 (Because side cannot be negative)
(Because side cannot be negative)
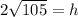
Therefore, the height of the isosceles triangle is
 cm. Approximate height is 20.49 cm.
cm. Approximate height is 20.49 cm.