Explanation:
A random variable X with a Gaussian distribution is supposed to be normally distributed. The normal distribution (shown in the attached figure below) is a continuous probability distribution that is symmetrical around its mean, and most of the values are observed to cluster around the central, forming the maximum point of the distribution, and the probabilities for the observed values decreases equally as it is further away from the mean.
The theoretical basis that provides the wide applications of the normal distribution is due to the central limit theorem, which basically states that as the sample size increases, the sampling distribution of the sampling means approximates a normal distribution. In other words, the distribution provided by sampling, given a sufficiently large sample size, will reflect the actual population distribution. Hence, this implies that we can use the normal distribution as a model to quantify variabilities in the case of constructing inferences about a population mean based on the sample mean.
The normal distribution is defined by only two parameters, namely the mean and standard deviation. The mean is the central tendency of the normal distribution and determines the peak for the distribution as most values cluster around the mean. Moreover, the standard deviation, generally, measures the spread of the data. It defines the width of the normal distribution and thus represents the distinctive distance of values from the mean.
In statistics, the empirical rule is a quick way to approximate probabilities of observations that lie within an estimated interval in a normal distribution. It states that for a normally distributed random variable
 ,
,
- 68.27% of the data lies within one standard deviation of the mean.
- 95.45% of the data lies within two standard deviations of the mean.
- 99.73% of the data lies within three standard deviations of the mean.
In mathematical notation, as shown in the figure below (for a standard normal distribution), the empirical rule is described as
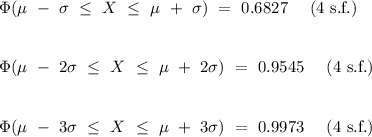
where the symbol
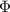 (the uppercase greek alphabet phi) is the cumulative density function of the normal distribution,
(the uppercase greek alphabet phi) is the cumulative density function of the normal distribution,
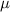 is the mean and
is the mean and
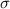 is the standard deviation of the normal distribution.
is the standard deviation of the normal distribution.