Question

An object is projected from a height of 100m above the ground at an angle of 300to the

horizontal with a velocity of 100m/s.
Calculate
(4)
(4)
The maximum height reached above the ground
Time of flight
The velocity and the direction of the object 1 sec before it hit the ground
(4)​

Answer 1

a) y = 127.6 m, b) 11.9s, c) v = 103.6 m / s, θ’= 326.7º

Step-by-step explanation:

This is a missile throwing exercise

let's start by breaking down the initial velocity

sin 30 =
`(v_(oy) )/(v_o)`

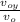
cos 30 = v₀ₓ / v₀

v_{oy} = v₀ go sin 30

v₀ₓ = v₀ cos 30

v_{oy} = 100 sin 30 = 50 m / s

v₀ₓ = 100 cos 30 = 86.6 m / s

a) the maximum height is requested.

At this point the vertical velocity is zero (v_y = 0)

v_y² =
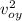`v_(oy)^2` - 2 g y

0 = v_{oy}^2 - 2g y

y =
`(v_(oy)^2 )/(2g)`

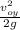
y = 50² / (2 9.8)

y = 127.6 m

b) Flight time

this is the time it takes to reach the ground, the reference system for this movement is taken on the ground this is a height of y = 0 m and the body is at an initial height of i = 100m

y = y₀ + v₀ t - ½ g t²

0 = 100 + 50 t - ½ 9.8 t²

we solve the quadratic equation

4.9 t² - 50 t - 100 = 0

t =
`(50 \pm √(50^2 + 4 \ 4.9 \ 100) )/(2 \ 4.9)`

t =
`(50 \ \pm \ 66.8)/(9.8)`

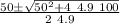
t₁ = 11.9 s

t₂ = -8.4 s

flight time is 11.9s

c) The time 1 s before hitting the ground is

t1 = 11.9 -1

t1 = 10.9 s

let's find the vertical speed

v_y =
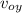`v_(oy)` - g t

v_y = 50 - 9.8 10.9

v_y = -56.8 m / s

the negative sign indicates that the direction of the velocity is downward.

On the x-axis there is no acceleration therefore the speed is constant.

Let's use the Pythagorean theorem

v =
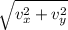
`√(v_x^2+v_y^2)`

v =
`\sqrt { 86.6^2 + 56.8^2}`

v = 103.6 m / s

let's use trigonometry

tan θ =
`(v_y)/(v_x)`

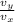
θ = tan⁻¹ \frac{v_y}{v_x}

θ = tan⁻¹ (-56.8 / 86.60)

θ = -33.3º

the negative sign indicates that it is measured clockwise from the x-axis

for a counterclockwise measurement

θ’= 360 - θ

θ' = 360 - 33.3

θ’= 326.7º