Answer:
The probability that the spark plugs are supposed to have a gap between 3.9mm and 4.3mm.
P(3.9≤X≤4.3) = 0.9922
Explanation:
Step(i):-
Given that the mean of the Normal distribution = 4.1mm
Given that the standard deviation of the Normal distribution = 0.0075mm
Let 'X' be the random variable in a normal distribution
Given that X₁ = 3.9mm
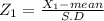
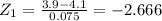
Given that X₂ = 4.3mm

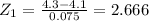
Step(ii):-
The probability that the spark plugs are supposed to have a gap between 3.9mm and 4.3mm.
P(3.9≤X≤4.3) = P(-2.666≤Z≤2.666)
= P(Z≤2.666)-P(Z≤-2.666)
= 0.5 +A(2.666) - (0.5-A(2.666)
= 2 × A(2.666)
= 2×0.4961
= 0.9922
Final answer:-
The probability that the spark plugs are supposed to have a gap between 3.9mm and 4.3mm.
P(3.9≤X≤4.3) = 0.9922