Question

A person places $123 in an investment account earning an annual rate of 2.8%,

compounded continuously. Using the formula V = Pert, where V is the value of the
account in t years, P is the principal initially invested, e is the base of a natural
logarithm, and r is the rate of interest, determine the amount of money, to the
nearest cent, in the account after 2 years.

Answer 1

V = 130.08

Explanation:

To solve we will use the equation V=
`Pe^r^t`

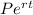
V= what you are solving for

P= initial number ( 123)

R= rate (2.8%)

-we can convert the rate to a decimal by moving the decimal place 2 spaces to the left.

R= 0.028

T= time (2 years)

The equation should be...
`V=123e^(^0^.^0^2^8^*^2^)`

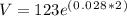
To solve we can first multiply 0.028 and 2

This is = 0.056

`V=123e^0^.^0^5^6`

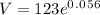
Then using a calculator we get...

V = 130.0845