Question

According to the latest real estate report from a suburban town, the mean number of home purchases during last quarter was 175 homes with a population standard deviation of 6 homes. A real estate agent believes that the recent increase of mortgage interest rates is causing a decline in home purchases. To test this, the real estate agent randomly selects 60 recent home purchases. What is the probability that the mean of this sample of home purchases is between 173 and 174 homes

Answer 1

The probability that the mean of this sample of home purchases is between 173 and 174 homes

P(173≤X≤174) = 0.0936

Explanation:

Step(i):-

Given that the mean of the Population = 175

Given that the standard deviation of the Population = 6

Let 'x⁻' be the mean of the random sample

Given that x₁⁻ = 173

`Z_(1) = (x^(-)-mean )/((S.D)/(√(n) ) ) = (173-175)/((6)/(√(60) ) ) =-2.58`

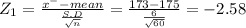
Given that x₂⁻ = 174

`Z_(2) = (x^(-)-mean )/((S.D)/(√(n) ) ) = (174-175)/((6)/(√(60) ) ) = -1.29`

Step(ii):-

The probability that the mean of this sample of home purchases is between 173 and 174 homes

P(X₁≤X≤X₂) = P(Z₁≤Z≤Z₂)

= P(Z≤Z₂) - P(Z≤Z₂) ( both values 'Z' values are negative)

= 0.5 -A(Z₁) - (0.5 -A(Z₂))

= |A(Z₂) -A(Z₁)|

P(173≤X≤174) = | A(2.58)-A(1.29)|

= 0.4951 - 0.4015 (∵ from normal table)

= 0.0936

Final answer:-

The probability that the mean of this sample of home purchases is between 173 and 174 homes

P(173≤X≤174) = 0.0936