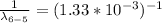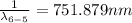Answer:

Step-by-step explanation:
From the question we are told that
Light wavelength
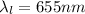
Light wavelength atom fall
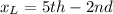
Photon wavelength
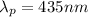
Photon wavelength atom fall

Generally the equation for the reciprocal of wavelength of emitted photon is is mathematically given by
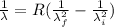
Therefore for initial drop of 5th to 2nd

Therefore for initial drop of 6th to 2nd
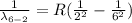
Generally we subtract (5th to 2nd) from (6th to 2nd)

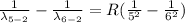
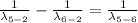
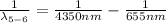
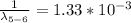
Therefore for 6th to 5th stage is mathematically given by