Answer:
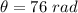
Step-by-step explanation:
Hoven that,
Initial angular velocity of the wheel = 24 rad/s
Final angular velocity = 14 m/s
Time, t = 4 s
We need to find how many radians does the wheel turn through during the 4 s interval. Let the displacement is
 . Using second equation of rotational kinematics to find it such that,
. Using second equation of rotational kinematics to find it such that,
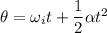
Where
 is angular acceleration
is angular acceleration
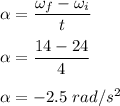
So,
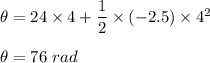
So, it will turn 76 radian during the 4 s interval.