Question

1. A company has a cash portfolio measured in millions. The drift is 0.1 per month, variance is 0.16per month. The initial cash is 2.0. a) Find the probability distribution after 6 months and after 1 year. b) Find the probability of a negative cash position at the end of 6 months and the end of 1 year. c) At what time in the future is the probability of a negative distribution greatest.

Answer 1

Explanation:

From the information given:

The probability distribution at the end of 6 months is determined as follows:

After 6 months;

Mean of probability distribution = value of Initial cash +
`\alpha`T

=2.0 +(0.1 × 6)

=2.6

After 6 months;

The probability distribution's standard deviation is estimated by using the following formula:

Standard deviation:

`= b√(T)`

`= 0.4 * √(6)`

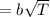
= 0.9798

Hence, after 6 months;

The company's cash position is supposed to be allocated monthly, with the following expenses.

Mean 2.6

Standard deviation 0.9798

Variance 0.96

After 12 months, the probability distribution is as follows:

Mean = value of Initial cash +
`\alpha`T

= 2.0 +(0.1 × 12)

= 3.2

The standard deviation is:

The standard deviation of probability distribution =
`b √(T)`

`= 0.4 * √(12)`

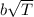
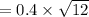
= 1.3856

Hence, after 6 months;

The company's cash position is supposed to be allocated monthly, with the following expenses.

Mean 3.2

Sandard deviation 1.3856

Variance 1.92

b)

in 6-month distribution, the probability of the negative value of the cash position is as follows.

Now, for us to find the negative cash distribution;

We need to estimate the z -scores value.

The z-score inform us greatly on the concept of how far a particular data point is from the mean.

For a normal distribution;

`z = (x-\mu)/(\sigma)`

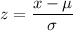
Here;

the value of x = zero as a result that if it exceeds zero. the cash position will be negative.

∴

`z = (x-\mu)/(\sigma)`

`z = (0 - 2.6)/(0.9798)`

`z = -2.6536`

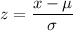
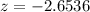
Using the standard distribution tables, it is now possible to calculate that the likelihood N(-2.65) equals 0.004 or 0.4 percent.

As a result, there's a 0.4 percent chance of getting a negative cash balance after six months.

For 12 months distribution:

The Probability of negative cash position is calculated as follows:

`z = (x-\mu)/(\sigma) \\ \\ z = (0-3.2)/(1.3856) \\ \\ z = -2.3094`

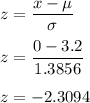
Using the standard distribution tables,

N(-2.31) equals 0.0104 or 1.04 percent.

As a result, there's a 1.04 percent chance of getting a negative cash balance after 1 year

c) To determine the time period over which the likelihood of achieving a negative cash condition is highest, it's necessary to examine the z-score more closely. Essentially, the z-score measures the difference between a given value(x) and the mean of all potential values
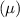`(\mu)`, expressed in terms of the total set's standard deviation
`(\sigma)`

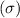
This suggests that the higher the z-score, the greater the difference occurring between x and
`\mu`, and thus the likelihood of receiving x is minimal. As a result, the best chance of finding a certain value is when the z-score is the lowest.

To do so, calculate the derivative of the z-score in relation to the time interval. The point where the derivative is equivalent to zero is where the z-scores are at their lowest.

The first step is to go over the z-score formula in more detail, as seen below.;

`z = (x-\mu)/(\sigma) \\ \\ z = (0-(initial \ value + \alpha T))/(b √(T)) \\ \\ z = (-initial \ value )/(b√(T))-(a √(T))/(b) \\ \\`

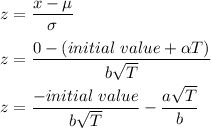
Now, compute the derivative of this equation with respect to T as follows:

`(dz)/(dT)= \frac{initial \ value * T^{-(3)/(2)}}{2b} - \frac{aT^{-(1)/(2)}}{2b}`

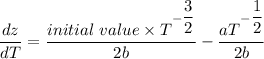
Now, figure out the value of T at which this derivative is equal to zero by substituting all values as follows:

`0 = \frac{2.0 * T^{-(3)/(2)}}{2* 0.4}- \frac{0.1 * T^{-(1)/(2)}}{2 * 0.4} \\ \\ \\ 0.1 * T^{-(1)/(2)}= 2.0 * T^{-(3)/(2)} \\ \\ \\T = (2)/(0.1) \\ \\ \\ T = 20`

As a result, the time period in which achieving a negative cash condition is = 20 months.