Question

A box having a weight of 8 lb is moving around in a circle of radius rA = 2 ft with a speed of (vA)1 = 5 ft/s while connected to the end of a rope. If the rope is pulled inward with a constant speed of vr = 4 ft/s, determine the speed of the box at the instant rB = 1 ft. How much work is done after pulling in the rope from A to B? Neglect friction and the size of the box

Answer 1

W = 1.875 J

Step-by-step explanation:

For this exercise let's use the relationship between work and kinetic energy

W = ΔK

The kinetic energy of rotational motion is

K₀ = ½ I w²

we can assume that the box is small, so it can be treated as a point object, with moment of inertia

I = m rₐ²

angular and linear velocity are related

v = w r

w = v / r

we substitute in the equation, for point A

K₀ = ½ (m rₐ²) (v / rₐ)²

K₀ = ½ m v²

For the final point B, as the system is isolated the angular momentum is conserved

initial L₀ = Io wo

final L_f = I_f w_f

L₀ = L_f

I₀ w₀ = I_f w_f

(m rₐ²) w₀ = (m
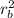`r_(b) ^2`) w_f

w_f = (rₐ/r_b)² w₀

with this value we find the final kinetic energy

K_f = ½ I_f w_f²

K_f = ½ (m
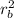`r_(b)^2`) ( (rₐ / r_b)² w₀) ²

K_f = ½ m
`(r_a^4)/(r_b^2) \ w_o^2`

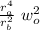
we substitute in the realcion of work

W = K_f - K₀

W = ½ m
`( \( \frac {r_a^2 }{r_b} )^2` w₀² - ½ m v²

W = ½ m
`(r_a^4)/(r_b^2) ( (v)/(r_a) ) ^2` - ½ m v²

W = ½ m
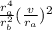`(r_a^2)/(r_b^2) \ v^2` - ½ m v2

W = ½ m v² ((
`( \ ((r_a)/(r_b))^2 -1)`

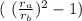
let's calculate

W = ½ (
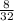`(8)/(32)` ) 5 ((2/1)² -1)

W = 0.625 (3)

W = 1.875 J