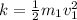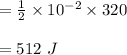Question

A 10 g bullet moving horizontally with a speed of 2000 m/s strikes and passes through a 4.0 kg block moving with a speed of 4.2 m/s in the opposite direction on a horizontal frictionless surface. If the block is brought to rest by the collision, what is the kinetic energy of the bullet as it emerges from the block. Round off your answer to zero decimal places.

Answer 1

The answer is "512 J".

Step-by-step explanation:

bullet mass
`m_1 = 10 g= 10^(-2) \ kg\\\\`

initial speed
`u_1 = 2\ (Km)/(s)= 2000\ (m)/(s)\\\\`

block mass
`m_2 = 4\ Kg`

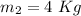
initial speed
`v_2 =-4.2 (m)/(s)`

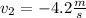
final speed
`v_2= 0`

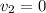
Let
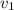`v_1` will be the bullet speed after collision:

throughout the consevation the linear moemuntum

`\to M_1V_1+m_2v_2=M_1U_1+m_2u_2\\\\\to (10^(-2) kg) V_1 +0 = (10^(-2) kg)(2000 (m)/(s)) + (4 \ kg)(-4.2 (m)/(s)) \\\\\ \to 10^(-2) v_1 = 20 -16.8\\\\`

`= 320 (m)/(s)`

The kinetic energy of the bullet in its emerges from the block

`k=(1)/(2) m_1 v_1^2`

`=(1)/(2) * 10^(-2) * 320\\\\=512 \ J`