Answer:
a) Longest wavelength is:

b) The frequency associated with this longest wavelength is:
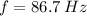
Step-by-step explanation:
a)
The wavelength equation of a standing wave is given by:
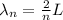
Where:
- L is the length of the string
- n is a natural number
We use n=1 to find the longest possible wavelength, so we will have:
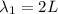

b)
The speed of the wave is given by:
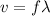
So we just need to find the f (frequency).
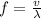
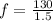
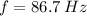
I hope it helps you!