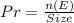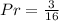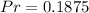Answer:
a
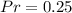
b
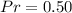
c
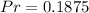
Explanation:
Given
 --- number of times
--- number of times
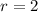 --- faces of a coin
--- faces of a coin
First, is to determine the sample size.
This is calculated as:
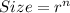
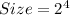

Solving (a): First and last slip is head
This event is represented as:

The probability is calculated as:
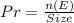
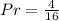
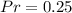
b) At least 2 consecutive flips that is heads.
This event is represented as:
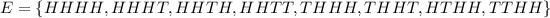
The probability is calculated as:
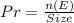

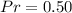
c) First is tail and at least 2 consecutive flips is head.
This event is represented as:
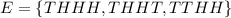
The probability is calculated as: