Question

The amount of flight time between failures of an airplane engine is exponentially distributed with mean 900 hours. If the engine is inspected every 600 hours of flight time, what is the probability that the engine will fail before it is inspected

Answer 1

0.4866 = 48.66% probability that the engine will fail before it is inspected

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

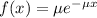
In which
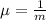`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X \leq x) = \int\limits^a_0 {f(x)} \, dx`

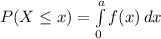
Which has the following solution:

`P(X \leq x) = 1 - e^(-\mu x)`

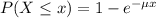
The probability of finding a value higher than x is:

`P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)`

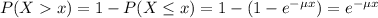
Exponentially distributed with mean 900 hours.

This means that
`m = 900, \mu = (1)/(900)`

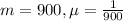
If the engine is inspected every 600 hours of flight time, what is the probability that the engine will fail before it is inspected?

This is
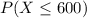`P(X \leq 600)`, which is:

`P(X \leq 600) = 1 - e^{-(600)/(900)} = 0.4866`

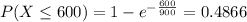
0.4866 = 48.66% probability that the engine will fail before it is inspected