Question

You apply for a job and have to take a drug test. You are curious about the error rate for the test so you do some research. You find a study where 47 out of 382 test results using this test were wrong (either a false positive or a false negative). The company that produces the drug test claims that less than 14% of the test results are wrong. Test if this seems accurate.

Answer 1

Test statistic Z = -1.0

|Z| = |-1.0| < 1.96 at 0.05 level of significance.

The null hypothesis is accepted

The company that produces the drug test claims that less than 14% of the test results are wrong

Explanation:

Step(i):-

Given that the population proportion P = 14% =0.14

Given that the sample size 'n' = 382 tests

Given that find a study where 47 out of 382 test results using this test were wrong (either a false positive or a false negative).

Sample proportion

`p = (x)/(n) = (47)/(382) = 0.1230`

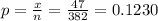
Null hypothesis: H₀ : P = 0.14

Alternative Hypothesis:H₁ : P≠ 0.14

Step(ii):-

Test statistic

`Z = \frac{p-P}{\sqrt{(PQ)/(n) } }`

`Z = \frac{0.1230-0.14}{\sqrt{(0.14 X0.86)/(382) } }`

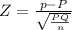
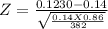
Z = - 1.0

|Z| = |-1.0| < 1.96 at 0.05 level of significance.

Final answer:-

The null hypothesis is accepted

The company that produces the drug test claims that less than 14% of the test results are wrong