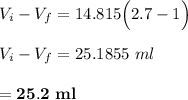Question

A beaker is filled with water. A small plastic container contains a solid bar of aluminum, which has a mass of 40 g, and is placed on the water so that it floats. The water level reads 60 ml. Next, the bar of aluminum is taken out of the container and placed in the water so that it sinks to the bottom. By how much does the water level change?

Answer 1

25.2 ml

Step-by-step explanation:

When the aluminium block is inserted in the container, the overall amount of only the water in the beaker can equal V o.

The weight of the water expelled by the plastic container should be equal to the weight of the aluminium block, according to the buoyancy balance relation.

i.e.

`\rho_w V_wg = m_(Al)g = \rho_(Al)V_(Al) g \\ \\ V_w = (\rho_(Al)V_(AL))/(\rho_(w))`

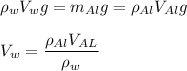
When the aluminium block is inserted into the plastic container, the initial volume of water = 60 ml

`V_i = V_o + V_w`

`V_i = V_o + (\rho_(Al)V_(Al))/(\rho_(w))---(1)`

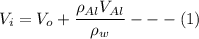
When the aluminium block is placed outside the container, the volume of the water

`V_f = V_o +V_(Al) ---(2)`

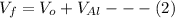
By subtracting equation (1) and (2)

`V_i -V_f = V_o + (\rho_(Al) V_(Al))/(\rho_w)- ( V_o + V_(Al)}) \\ \\ =(\rho _(Al)V_(Al))/(\rho_w)-V_(Al) \\ \\ = V_(Al) \Big( (\rho_(Al))/(\rho_(w))-1 \Big)`

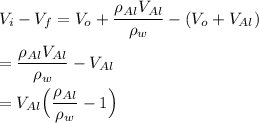
since;

`m_(Al) = 40 g`

`V _(Al) = (40 \ g)/(2.7 \ g/cm^3) \\ \\ V_(Al) = 14.815 \ cm^3`

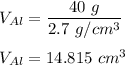
Similarly;

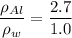
`(\rho_(Al))/(\rho_(w))= (2.7 )/(1.0)`

= 2.7

`V_i -V_f =14.815\Big( 2.7-1 \Big) \\ \\ V_i -V_f = 25.1855 \ ml \\ \\ = \mathbf{25.2 \ ml}`