Question

Help me with this, I was never taught how to do this...

Answer 1

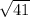`√(41)` = x

Explanation:

Basically, find the missing side lengths of each triangle so that you can solve for x:

1. right triangle w/ side lengths 48 and 52

• 48^2 + (missing side)^2 = 52^2
• 2304 + (missing side)^2 = 2704
• (missing side)^2 = 400
• (missing side) = 20 (use this for next triangle)

2. right triangle w/ side lengths 12 and 20 (from previous triangle)

• 12^2 + (missing side)^2 = 20^2
• 144 + (missing side)^2 = 400
• (missing side)^2 = 256
• (missing side) = 16 (will be used with next triangle's missing side)

3. right triangle w/ side lengths 5 and 13

• 5^2 + (missing side)^2 = 13^2
• 25 + (missing side)^2 = 169
• (missing side)^2 =144
• (missing side) = 12

Take right triangle w/ side lengths 12, 20, and 16 (#2) and right triangle w/ side lengths 5, 13, and 12 (#3):

• the value of 12 (missing side of #3) subtracted from the #2's missing side, 16, (not its hypotenuse that equals 20 which was found from #1) will equal the missing side length that will be used to find 'x'
• 16 - 12 = 4 ---> so the side lengths are 4, 5, and x

4. Solve for the final triangle that includes x:

• 4^2 + 5^2 = x^2
• 16 + 25 = x^2
• 41 = x^2
• 
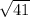  `√(41)` = x