Question

Canine Crunchies Inc. (CCI) sells bags of dog food to warehouse clubs. CCI uses an automatic filling process to fill the bags. Weights of the filled bags are approximately normally distributed with a mean of 45 kilograms and a standard deviation of 1.2 kilograms.

Requried:
a. What is the probability that a filled bag will weigh less than 49.5 kilograms?
b. What is the probability that a randomly sampled filled bag will weight between 48.5 and 51 kilograms?
c. What is the minimum weight a bag of dog food could be and remain in the top 15% of all bags filled?
d. CCI is unable to adjust the mean of the filling process. However, it is able to adjust the standard deviation of the filling process. What would the standard deviation need to be so that no more than 2% of all filled bags weigh more than 52 kilograms?

Answer 1

a) 0.9999 = 99.99% probability that a filled bag will weigh less than 49.5 kilograms

b) 0.0018 = 0.18% probability that a randomly sampled filled bag will weight between 48.5 and 51 kilograms.

c) 46.24 kilograms

d) The standard deviation would have to be of 3.41 kilograms.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Mean of 45 kilograms and a standard deviation of 1.2 kilograms.

This means that
`\mu = 45, \sigma = 1.2`

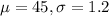
a. What is the probability that a filled bag will weigh less than 49.5 kilograms?

This is the pvalue of Z when X = 49.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (49.5 - 45)/(1.2)`

`Z = 3.75`

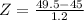
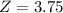
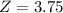`Z = 3.75` has a pvalue of 0.9999

0.9999 = 99.99% probability that a filled bag will weigh less than 49.5 kilograms

b. What is the probability that a randomly sampled filled bag will weight between 48.5 and 51 kilograms?

This is the pvalue of Z when X = 51 subtracted by the pvalue of Z when X = 48.5.

X = 51

`Z = (X - \mu)/(\sigma)`

`Z = (51 - 45)/(1.2)`

`Z = 5`

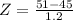
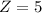
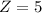`Z = 5` has a pvalue of 1

X = 48.5

`Z = (X - \mu)/(\sigma)`

`Z = (48.5 - 45)/(1.2)`

`Z = 2.92`

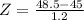
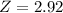
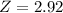`Z = 2.92` has a pvalue of 0.9982

1 - 0.9982 = 0.0018

0.0018 = 0.18% probability that a randomly sampled filled bag will weight between 48.5 and 51 kilograms.

c. What is the minimum weight a bag of dog food could be and remain in the top 15% of all bags filled?

This is the 100 - 15 = 85th percentile, which is X when Z has a pvalue of 0.85. So X when Z = 1.037

`Z = (X - \mu)/(\sigma)`

`1.037 = (X - 45)/(1.2)`

`X - 45 = 1.037*1.2`

`X = 46.24`

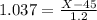
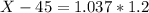
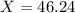
46.24 kilograms.

d. CCI is unable to adjust the mean of the filling process. However, it is able to adjust the standard deviation of the filling process. What would the standard deviation need to be so that no more than 2% of all filled bags weigh more than 52 kilograms?

X = 52 would have to be the 100 - 2 = 98th percentile, which is X when Z has a pvalue of 0.98, so X when Z = 2.054. We would need to find the value of
`\sigma` for this.

`Z = (X - \mu)/(\sigma)`

`2.054 = (52 - 45)/(\sigma)`

`2.054\sigma = 7`

`\sigma = (7)/(2.054)`

`\sigma = 3.41`

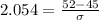
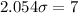
The standard deviation would have to be of 3.41 kilograms.