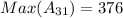Question

If you create a matrix, C, to show the inventory at the end of July, the value of the entry represented by C22 is ?

In a matrix with components aij, which represents unit sales for july, the maximum possible value that a31 can have is ?

Answer 1

`C_(22) = 389`

`Max(A_(31)) =376`

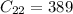
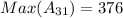
Explanation:

Given

See attachment for complete question

Solving (a): The entry C22

First, matrix C represents the inventory at the end of July.

The entry of C is calculated as:

`C = Inventory - Sales`

i.e.

`C = \left[\begin{array}{ccc}543&356&643\\364&476&419\\376&903&409\end{array}\right] - \left[\begin{array}{ccc}102&78&97\\98&87&59\\54&89&79\end{array}\right]`

`C = \left[\begin{array}{ccc}543-102&356-78&643-97\\364-98&476-87&419-59\\376-54&903-89&409-79\end{array}\right]`

`C = \left[\begin{array}{ccc}441&278&546\\266&389&360\\322&814&330\end{array}\right]`

Item C22 means the entry at the second row and the second column.

From the matrix

`C_(22) = 389`

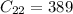
Solving (b): The maximum A31 possible.

From the given data, we have:

`Inventory = \left[\begin{array}{ccc}543&356&643\\364&476&419\\376&903&409\end{array}\right]`

`Unit\ Sales = \left[\begin{array}{ccc}102&78&97\\98&87&59\\54&89&79\end{array}\right]`

From the matrices above.

A31 means entry at the 3rd row and 1st column.

So, the possible values of A31 are:

`A_(31) = 376`

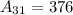
and

`A_(31) = 54`

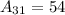
By comparison, 376 > 54

So:

`Max(A_(31)) =376`