Answer:
The sum of reciprocals is 2/3.
You don't need complex numbers to solve this, but if you try to find a and b you will need complex numbers.
Explanation:
a+b = 2
a*b = 3
1/a + 1/b = x
(a*b)*(1/a + 1/b) = (a*b)x
b + a = (a*b)(x)
2 = 3x
x = 2/3
b = 2 - a
a*(2 - a) = 3
-a^2 + 2a = 3
-a^2 + 2a - 3 = 0
a^2 - 2a + 3 = 0
let's solve the quadratic equation
a^2 - 2a + 3 = a^2 - 2a + 1 + 2 = (a - 1)^2 + 2 = 0
(a - 1)^2 = -2
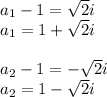
these options correspond to a and b from the original question.