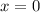Answer:
Explanation:
Given
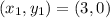
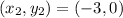
Required
The equation of the perpendicular bisector.
First, calculate the midpoint of the given endpoints
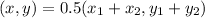
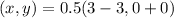
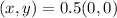
Open bracket

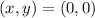
Next, determine the slope of the given endpoints.

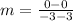

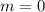
Next, calculate the slope of the perpendicular bisector.
When two lines are perpendicular, the relationship between them is:
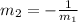
In this case:
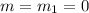
So:
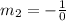
Since the slope is
 , the equation is:
, the equation is:

Where:
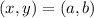
Recall that:
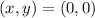
So:
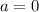
Hence, the equation is: