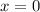Question

An equation of the perpendicular bisector of the line segment with end points (3,0) and (-3,0) is

A) x = -3/2
B) x = 0
C) x = 3/2
D) X = 3
E) X = 6
Help please with steps

Answer 1

`x = 0`

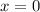
Explanation:

Given

`(x_1,y_1) = (3,0)`

`(x_2,y_2) = (-3,0)`

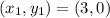
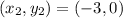
Required

The equation of the perpendicular bisector.

First, calculate the midpoint of the given endpoints

`(x,y) = 0.5(x_1 + x_2, y_1 + y_2)`

`(x,y) = 0.5(3-3, 0+ 0)`

`(x,y) = 0.5(0, 0)`

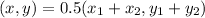
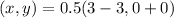
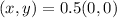
Open bracket

`(x,y) = (0.5*0, 0.5*0)`

`(x,y) = (0, 0)`

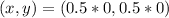
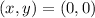
Next, determine the slope of the given endpoints.

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (0 - 0)/(-3- 3)`

`m = (0)/(-6)`

`m = 0`

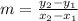
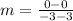
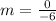
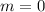
Next, calculate the slope of the perpendicular bisector.

When two lines are perpendicular, the relationship between them is:

`m_2 = -(1)/(m_1)`

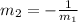
In this case:

`m = m_1 = 0`

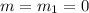
So:

`m_2 = -(1)/(0)`

`m_2 = unde\ fined`

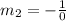
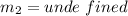
Since the slope is
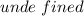`unde\ fined`, the equation is:

`x = a`

Where:

`(x,y) = (a,b)`

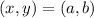
Recall that:

`(x,y) = (0, 0)`

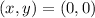
So:

`a = 0`

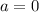
Hence, the equation is:

`x = 0`