Question

Physics question 28 plz help me

Answer 1

a. I = 30 A

b. E = 1080000 J = 1080 KJ

c. ΔT = 12.86°C

d. Cost = $ 4.32

Step-by-step explanation:

a.

The current in the coil is given by Ohm's Law:

`V = IR\\I = (V)/(R)`

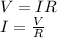
where,

I = current = ?

V = Voltage = 120 V

R = Resistance = 4 Ω

Therefore,

`I = (120\ V)/(4 \Omega)\\`

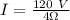
I = 30 A

b.

The energy can be calculated as:

`E = VIt\\E = (120\ V)(30\ A)(5\ min)((60\ s)/(1\ min))\\`

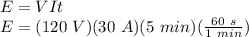
E = 1080000 J = 1080 KJ

c.

For the increase in the temperature of water:

`E = mC\Delta T\\`

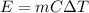
where,

m = mass of water = 20 kg

C = specific heat of water = 4.2 KJ/kg.°C

Therefore,

`1080\ KJ = (20\ kg)(4.2\ KJ/kg.^oC)\Delta T`

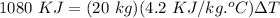
ΔT = 12.86°C

d.

First, we will calculate the total energy consumed:

`E=(Power)(Time)\\E=VI(Time)\\E = (120\ V)(30\ A)(0.5\ h/d)(30\ d)\\E = 54000\ Wh\\E = 54 KWh`

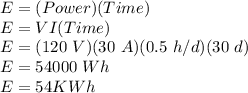
Now, for the cost:

`Cost = (Unit\ Cost)(Energy)\\Cost = (\$ 0.08\KWh)(54\ KWh)`

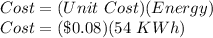
Cost = $ 4.32