Question

Studies have suggusted that twins, in their early years, tend to have lower IQs and pick up language more slowly than non-twins. The slower intellectual growth may be caused by benign parental neglect. Suppose it is desired to estimate the mean attention time given

to twins per week by their parents. A sample of 26 sets of two-year-old twin boys was taken, and after one week the attention time
received was recorded. The mean was found to be 27.4 hours with a standard deviation of 11,2 hours. Use this information to contruc
a 98% confidence interval for the mean attention time given to all twin boys by their parents, assuming that the population is
approximately normally distributed, Round the endpoints to one decimal place.
Confidence interval:( , )

Answer 1

Confidence interval: (21.9, 32.9).

Explanation:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

df = 26 - 1 = 25

98% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 25 degrees of freedom(y-axis) and a confidence level of
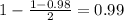`1 - (1 - 0.98)/(2) = 0.99`. So we have T = 2.485

The margin of error is:

`M = T(s)/(√(n)) = 2.485(11.2)/(√(26)) = 5.5`

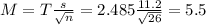
In which s is the standard deviation of the sample and n is the size of the sample.

The lower end of the interval is the sample mean subtracted by M. So it is 27.4 - 5.5 = 21.9 hours

The upper end of the interval is the sample mean added to M. So it is 27.4 + 5.5 = 32.9 hours

Confidence interval: (21.9, 32.9).