Question

Part A: To the nearest tenth of an inch, what was the circumference of the circular pie before the slice was

cut out?
Part B: To the nearest inch, what was the area of the circular pie before the slice was cut out?
Part C: To the nearest tenth of an inch, what is the area of the slice of pie that was cut out?
Part D: To the nearest inch, what is the length of the curst for the slice of pie that was cut out?
Next Question
Question 1 of 2

Answer 1

Part A

The circumference of the circular pie before the slice was cut out is approximately 69.1 inches

Part B; The area of the circular pie before the slice was cut out is approximately 380 in.²

Part C

The area of the slice of pie that was cut out in approximately 40 in.²

Part D;

The length of the crust for the slice of pie is approximately 7 inches

Explanation:

Part A

The shape of the pie = Circular shape

The radius of the pie, r = 11 inches

The circumference of a circle = 2·π·r

Therefore, we have;

The circumference of the circular pie before the slice was cut out, 'C', is given as follows;

Where;

r = 2 inches

C = 2 × π × 11 inches = 22·π inches ≈ 69.115 inches

The initial circumference of the circular, C ≈ 69.115 inches

To the nearest tenth of an inch, we have;

The initial circumference of the circular, C ≈ 69.1 inches

Part B; The area of a circle, A = π·r²

Therefore;

For the circular pie before the slice was cut out, A = π·(11 in.)² ≈ 380.133 in.²

To the nearest square inch, we have;

The area of the circular pie before the slice was cut out, A ≈ 380 in.²

Part C

The area of the slice of the pie that was cut out, A is given by the area of a sector of a circle as follows;

`The \ area \ of \ a \ sector, A = (\theta)/(360 ^(\circ)) * \pi \cdot r^2`

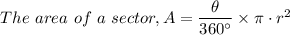
The angle of the sector formed by the slice of pie that was cut out, θ = 38°

Therefore, the area of the slice of pie that was cut out, 'A', to the nearest tenth of a square inch is given as follows;

A = 38/360 × π × (11 in.²) = 40 in.²

The area of the slice of pie that was cut out, A = 40 in.²

Part D;

The length of the crust of the slice of pie that was cut out is given by the arc length of the sector of the circular pie the slice of pie represent as follows;

`Arc \ length = (\theta)/(360 ^(\circ)) * 2\cdot \pi \cdot r`

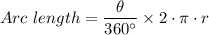
Therefore for the slice of pie, to the nearest inch, we have;

`Arc \ length = (38 ^(\circ))/(360 ^(\circ)) * 2* \pi * 11 \, in. \approx 7 \, in.`

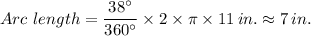
The length of the crust for the slice of pie ≈ 7 in.