Question

If the cost, C(x), for manufacturing x units of a certain product is given by

C(x) = x2 – 15x + 34
find the number of units manufactured at a cost of $8350.

Answer 1

99 units.

Explanation:

The cost function for manufacturing x units of a certain product is:

`C(x)=x^2-15x+34`

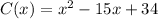
We want to find the number of units manufactured at a cost of $8350. Therefore:

`8350=x^2-15x+34`

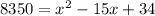
Subtract 8350 from both sides:

`x^2-15x-8316=0`

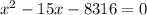
This equation can be a bit difficult to factor, if even possible, so we can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

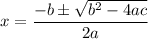
In this case, a = 1, b = -15, and c = -8316. Thus:

`\displaystyle x=(-(-15)\pm√((-15)^2-4(1)(-8316)))/(2(1))`

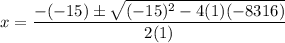
Simplify:

`\displaystyle x=(15\pm√(33489))/(2)`

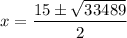
Evaluate:

`\displaystyle x=(15\pm183)/(2)`

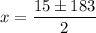
Therefore, our solutions are:

`\displaystyle x=(15+183)/(2)=99\text{ and } x=(15-183)/(2)=-84`

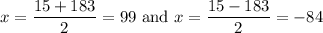
We cannot produce negative items, so we can ignore the second answer.

Therefore, for a cost of $8350, 99 items are being produced.