Answer:
The table does not represent a proportional relationship because the ratio of the y-values to the corresponding x-value at each data point is not constant
y/x ≠ Constant
Explanation:
The table of values for the total cost in dollars (y) to join a gym for "x" number of months is presented as follows;
x; 1, 2, 3, 4, 5
y; 25, 40, 55, 70, 85
The rate of change of the data in the table is given by the following formula;
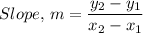
Between the 1st and the 3rd point, we have;
m = (55 - 25)/(3 - 1) = 15
Between the 1st and the 5th point, we have;
m = (85 - 25)/(5 - 1) = 15
Therefore, the rate of change of the y values per unit change of the x-value is 15
Therefore, the "x" and y-values have a linear relationship
However, for a proportional relationship, we have;
y/x = Constant
At the 1st point, we have;
25/1 = 25
At the 3rd point, we have;
55/3 = 18.
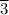
∴ y/x is not constant and the the data in the table does not represent a proportional relationship.