Question

What is the correct formula to find the sum of the finite geometric series below?


`\displaystyle 2 + (2)/(3) + (2)/(9) + \ ... \ + (2)/(3^6)`

Answer 1

Explanation:

`\tt2 + (2)/(3) + \frac{2}{ {3}^(2) } + \frac{2}{ {3}^(3) } + \frac{2}{ {3}^(4) } + \frac{2}{ {3}^(5) } + \frac{2}{ {3}^(6) }`

r =
`\tt{a_2 / a_1}`

r =
`\tt{(2)/(3) / 2}`

r =
`\tt{\bold{(1)/(3)}}`

Soo :

`\sf s_n = \frac{a( {r}^(n) - 1) }{r - 1}`

`\sf s_7 = \frac{2(( (1)/(3) ) {}^(7 - 1) - 1) }{( (1)/(3) - 1) }`

`\sf s_7 \approx \bold{ \underline{2.97}}`

Answer 2

We are given the Geometric Series:

`2 + (2)/(3) + (2)/(9) + (2)/(27) + (2)/(81) + (2)/(243) + (2)/(729)`

which can be rewritten as:

`2 + (2)/(3) + (2)/(3^(2) ) + (2)/(3^(3)) + (2)/(3^(4)) + (2)/(3^(5)) + (2)/(3^(6))`

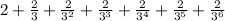
here, we can see that every term is (1/3) times the last term

Hence, we can say that the common ratio of this Geometric Series is 1/3

Finding the Sum:

We know that the sum of a Geometric Series is:

`S_(n) = (a(r^(n)-1))/(r-1)`

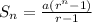
(where r is the common ratio, a is the first term, and n is the number of terms)

another look at the given Geometric Series tells us that the first term is 2 and the number of terms is 7

plugging these values in the formula, we get:

`S_(n) = (2((1/3)^(7)-1))/((1/3)-1)`

`S_(n) = (-1.99)/(-0.67)`

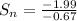
Sₙ = 2.97