The correct answer is B)
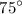 .
.
In an isosceles triangle, the two base angles are congruent.
So in this triangle,
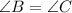 .
.
The sum of the angles in a triangle is
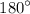 , so we have:
, so we have:
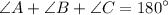 .
.
Substituting in what we know about
 , we get:
, we get:
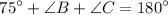
Since
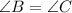 , we can rewrite this as:
, we can rewrite this as:
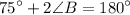
Solving for
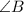 , we get:
, we get:
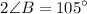
Therefore
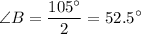
However, we know that
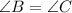 , so
, so
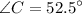 as well.
as well.
Therefore, the measure of
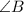 is
is
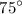 .
.