Question

Find the seventh term of the geometric sequence if a1 = 7 and r = 3

Answer 1

The seventh term is 5,103.

Step-by-step explanation:

Hey there!

We're given the initial term and the common ratio of an undetermined geometric sequence.

The formula to determine a geometric sequence is
`x_n = ar^((n-1))`.

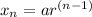We know that a₁ is 7 and that r is 3. However, we don't know what n is. Our variable n is a stand in for the position in the sequence. Since we want 7 terms, we are going to have terms 1, 2, 3, 4, 5, 6, and 7. The variable n will equal each one of these.

Finally, our term xₙ is equivalent to the term we are trying to find, so it is a standalone variable.

Let's find all seven terms using the above formula.

We already have our first term: 7. Therefore, we set n equal to 2 and solve for xₙ.

Term 2

`x_n = 7(3)^((2-1))\\x_n = 7(3)^1\\x_n = 7(3)\\x_n = 21`

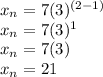
Term 3

`x_n = 7(3)^((3-1))\\x_n = 7(3)^2\\x_n = 7(9)\\x_n = 63`

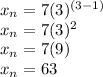
Term 4

`x_n = 7(3)^((4-1))\\x_n = 7(3)^3\\x_n = 7(27)\\x_n = 189`

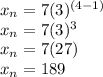
Term 5

`x_n = 7(3)^((5-1))\\x_n = 7(3)^4\\x_n = 7(81)\\x_n = 567`

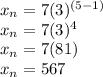
Term 6

`x_n = 7(3)^((6-1))\\x_n = 7(3)^5\\x_n = 7(243)\\x_n = 1701`

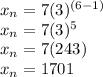
Term 7

`x_n = 7(3)^((7-1))\\x_n = 7(3)^6\\x_n = 7(729)\\x_n = 5103`

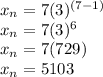
We have found the seventh term to be 5,103.

The sequence is written as 7, 21, 63, 189, 567, 1,701, 5,103... (it will be ongoing if you wanted to calculate the next term).