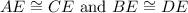Question

Heya! ツ

☛
`\underline{ \underline{ \text{question}}}` : In the given figure , O is the centre of the circle. Two equal chords AB and CD intersect each other at E. Prove that :
i. AE = CE
ii. BE = DE

*Random/irrelevant answers will not be tolerated !

Answer 1

See Below.

Explanation:

In the given figure, O is the center of the circle. Two equal chords AB and CD intersect each other at E.

We want to prove that I) AE = CE and II) BE = DE

First, we will construct two triangles by constructing segments AD and CB. This is shown in Figure 1.

Recall that congruent chords have congruent arcs. Since chords AB ≅ CD, their respective arcs are also congruent:

`\stackrel{\frown}{AB }\, \cong\, \stackrel{\frown}{CD}`

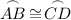
Arc AB is the sum of Arcs AD and DB:

`\stackrel{\frown}{AB}=\stackrel{\frown}{AD}+\stackrel{\frown}{DB}`

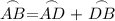
Likewise, Arc CD is the sum of Arcs CB and DB. So:

`\stackrel{\frown}{CD}=\stackrel{\frown}{CB}+\stackrel{\frown}{DB}`

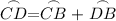
Since Arc AB ≅ Arc CD:

`\stackrel{\frown}{AD}+\stackrel{\frown}{DB}=\stackrel{\frown}{CB}+\stackrel{\frown}{DB}`

Solve:

`\stackrel{\frown}{AD}\, \cong\,\stackrel{\frown}{CB}`

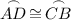
The converse tells us that congruent arcs have congruent chords. Thus:

`AD\cong CB`

Note that both ∠ADC and ∠CBA intercept the same arc Arc AC. Therefore:

`\angle ADC\cong \angle CBA`

Additionally:

`\angle AED\cong \angle CEB`

Since they are vertical angles.

Thus:

`\Delta AED\cong \Delta CEB`

By AAS.

Then by CPCTC:

`AE\cong CE\text{ and } BE\cong DE`

Answer 2

this is your answer. look it once.