Given:
The quadratic equation is:
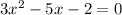
To find:
Point that is the solution of given equation.
Solution:
We have,
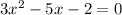
The quadratic function of the above equation is:
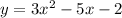
Putting
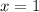 , we get
, we get
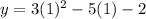
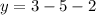
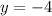
The function passes through the point (1,-4). It means (1,-4) is the solution of given equation but (1,5) is not a solution of given equation.
Therefore, the correct option is A.