Question

Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.

About the y-axis
Choices:
(128/3)π
(64/3)π
64π
32π

Answer 1

ok

Explanation:

Answer 2

Using the shell method, the volume of the solid generated by revolving the shaded region about the y-axis, given by
`\(y = 4x - x^2\), is \((128)/(3)\pi\)`. Thus, the correct answer is A.

To find the volume of the solid generated by revolving the shaded region about the y-axis using the shell method, we'll integrate along the y-axis.

The equation
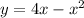`\(y = 4x - x^2\)` can be rewritten as
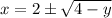`\(x = 2 \pm √(4 - y)\)`. To find the limits of integration, we need to determine the points where the curves intersect:

`\[4x - x^2 = 0\]`

Factoring out x, we get
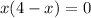`\(x(4 - x) = 0\)`. So,
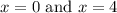`\(x = 0\) and \(x = 4\)` are the points of intersection.

Now, the radius of the shell is the distance from the y-axis to the curve, which is x. The height of the shell is the differential change in y, denoted as dy.

The volume element of a shell is
`\(V_{\text{shell}} = 2\pi x \, dy\)`.

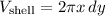Now, integrate
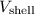`\(V_{\text{shell}}\)` from
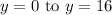`\(y = 0\) to \(y = 16\)` (the square of
`4`):

`\[V = \int_(0)^(16) 2\pi x \, dy\]\[V = \int_(0)^(16) 2\pi(2 + √(4 - y)) \, dy\]`

Evaluate this integral to find the volume.

`\[V = \int_(0)^(16) 2\pi(2 + √(4 - y)) \, dy = (128)/(3)\pi\]`

Therefore, the correct answer is A.
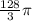`\((128)/(3)\pi\)`.