Answer:
- The population in 2001 is 23.1 million
- It will reach 28.3 million in 2013
Explanation:
Given
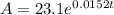
Solving (a): Population in 2000.
This implies that
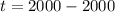
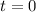
So, we have:
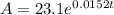
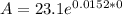
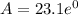
Solve the exponent
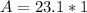

The population in 2001 is 23.1 million
Solving (b): When will it reach 28.3 million
This implies that:
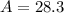
So, we have:
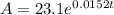
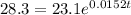
Divide both sides by 23.1

Take natural logarithm of both sides
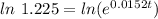
Rewrite as:
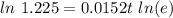
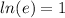
So:

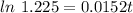
Make t the subject
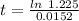
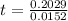
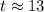
Add the value of t to 2013 to get the actual year
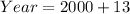
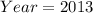
It will reach 28.3 million in 2013