Question

Select the correct answer.

If function g has the factors (x - 7) and (x + 6), what are the zeros of function g?
OA. -7 and 6
OB. -6 and 7
OC. 6 and 7
OD
-7 and -6

Answer 1

Given:

A function g has the factors (x - 7) and (x + 6).

To find:

The zeros of the function g.

Solution:

We know that if (x-a) is a factor of a function then x=a is a zero of that function because

`x-a=0`

`x=a`

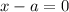
It is given that the function g has the factors (x - 7) and (x + 6).

`x-7=0`

`x=7`

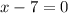
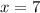
Similarly,

`x+6=0`

`x=-6`

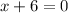
Therefore, -6 and 7 are two zeros of the function g.

Hence the correct option is B.