Question

Find the area of the sector

Answer 1

The easiest way to do this is to calculate the Area of the whole circle and then subtract the 1/4 of the missing piece.

So:

• A=pi×81
• and then pi×81/4
• and then pi×81-[pi×81/4]

Answer 2

`\boxed {\boxed {\sf a \approx 190.9 \ yd^2}}`

Explanation:

There are 2 formulas for the area of a sector, but since we are given the central angle in degrees (not radians), we will use this formula:

`a= \frac {\theta}{360} * \pi r^2`

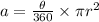
Where θ is the central angle and r is the radius.

For this circle, the radius is 9 yards and the central angle is 270 degrees. We can substitute these values into the formula.

`a= \frac {270}{360} * \pi * (9 \ yd )^2`

Solve the fraction.

`a=0.75 * \pi * (9 \ yd)^2`

Solve the exponent.

• (9 yd)²= 9 yd* 9 yd=81 yd²

`a= 0.75 * \pi * 81 \ yd^2`

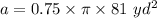
Multiply all three numbers together.

`a= 190.851753706 \ yd^2`

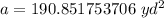
The question asks us to round to the nearest tenth.

• 190.851753706

The 5 in the hundredth place tells us to round the 8 up to a 9.

`a \approx 190.9 \ yd^2`

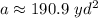
The area of the sector is approximately 190.9 square yards.