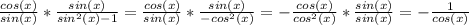Answer:
First, we know that:
cot(x) = cos(x)/sin(x)
csc(x) = 1/sin(x)
I can't know for sure what is the exact equation, so I will assume two cases.
The first case is if the equation is:
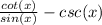
if we replace cot(x) and csc(x) we get:
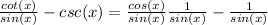
Now let's we can rewrite this as:


We can't simplify it more.
Second case:
If the initial equation was
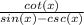
Then if we replace cot(x) and csc(x)
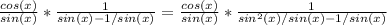
This is equal to:

And we know that:
sin^2(x) + cos^2(x) = 1
Then:
sin^2(x) - 1 = -cos^2(x)
So we can replace that in our equation: