Question

5 Exam-style ABCD is a kite.

The coordinates of A are (−1, 3).
The equation of the diagonal BD is y = 3x − 1.
Find the equation of the diagonal AC.

Answer 1

let's recall that in a Kite the diagonals meet each other at 90° angles, Check the picture below, so we're looking for the equation of a line that's perpendicular to BD and that passes through (-1 , 3).

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of BD

`y = \stackrel{\stackrel{m}{\downarrow }}{3}x-1\impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

`\stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{3\implies \cfrac{3}{1}} ~\hfill \stackrel{reciprocal}{\cfrac{1}{3}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{1}{3}}}`

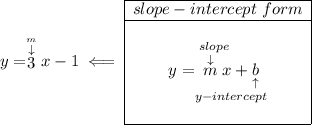
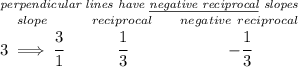
so we're really looking for the equation of a line whose slope is -1/3 and passes through point A

`(\stackrel{x_1}{-1}~,~\stackrel{y_1}{3})\qquad \qquad \stackrel{slope}{m}\implies -\cfrac{1}{3} \\\\\\ \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{-\cfrac{1}{3}}[x-\stackrel{x_1}{(-1)}]\implies y-3=-\cfrac{1}{3}(x+1) \\\\\\ y-3=-\cfrac{1}{3}x-\cfrac{1}{3}\implies y=-\cfrac{1}{3}x-\cfrac{1}{3}+3\implies y=-\cfrac{1}{3}x+\cfrac{8}{3}`