Question

Two alloys A and B are being used to manufacture a certain steel product. An experiment needs to be designed to compare the two in terms of maximum load capacity in tons (the maximum weight that can be tolerated without breaking). It is known that the two standard deviations in load capacity are equal at 5 tons each. An experiment is conducted in which 30 specimens of each alloy (A and B) are tested and the results recorded as follows:

x¯A = 49.5, x¯B = 45.5, x¯A − x¯B = 4
The manufacturers of alloy A are convinced that this evidence shows conclusively that muA & muB and strongly supports the claim that their alloy is superior. Manufacturers of alloy BB claim that the experiment could easily have given x¯A − x¯B = 4 even if the two population means are equal. In other words, "the results are inconclusive!"
(a) Make an argument that manufacturers of alloy B are wrong. Do it by computing
P(x¯A − x¯B > 4 | muA - muB
(b) Do you think these data strongly support alloy A?

Answer 1

Explanation:

From the given information, we can compute the table showing the summarized statistics of the two alloys A & B:

Alloy A Alloy B

Sample mean
`\bar {x} _A = 49.5`
`\bar {x} _B = 45.5`

Equal standard deviation
`\sigma_A = 5`
`\sigma_B= 5`

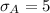
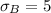
Sample size
`n_A = 30`
`n_(B)= 30`

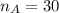
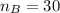
Mean of the sampling distribution is :

`\mu_{\bar{X_1}-\bar{X_2}}= 49.5-45.5 \\ \\ = 4.0`

Standard deviation of sampling distribution:

`\sigma_{\bar{x_1}-\bar{x_2} }= \sqrt{\sigma^2_{\bar{x_1}-\bar{x_2} }} \\ \\ = \sqrt{(\sigma_1^2)/(n_1) + (\sigma^2_2)/(n_2) } \\ \\ =\sqrt{(25)/(30)+(25)/(30)} \\\\=√(1.667) \\ \\ =1.2909`

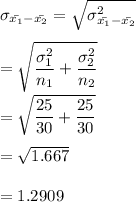
Hypothesis testing.

Null hypothesis:
`H_o: \mu_A -\mu_B = 0`

Alternative hypothesis:
`H_A:\mu_A -\mu_B > 4`

The required probability is:

`P(\overline X_A - \overline X_B>4|\mu_A - \mu_B) = P\Big (((\overline X_A - \overline X_B)-\mu_(X_A-X_B))/(\sigma_(\overline x_A -\overline x_B)) > (4 - \mu_(X_A-\overline X_B))/(\sigma _(\overline x_A - \overline X_B)) \Big) \\ \\ = P \Big( z > (4-0)/(1.2909)\Big) \\ \\ = P(z \ge 3.10)\\ \\ = 1 - P(z < 3.10) \\ \\ \text{Using EXCEL Function:} \\ \\ = 1 - [NORMDIST(3.10)] \\ \\ = 1- 0.999032 \\ \\ 0.000968 \\ \\ \simeq 0.0010`

This implies that a minimal chance of probability shows that the difference of 4 is not likely, provided that the two population means are the same.

b)

Since the P-value is very small which is lower than any level of significance.

Then, we reject
`H_o` and conclude that there is enough evidence to fully support alloy A.