Answer:
the required expression is
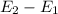 = 4[ 1 -
= 4[ 1 -
 ]
]
Explanation:
Given the data in the question;
Q = -0.2[ 1 -
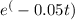 ]
]
ω = 100 rad/s
Torque T = 18 N-m
Electric power input = 2.0 kW
now, form the first law of thermodynamics;
dE/dt = dQ/dt + dw/dt = Q' + w'
dE/dt = Q' + w' ------ let this be equation 1
w' is the net power on the system
w' =
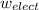 -
-
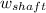
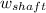 = T × ω
= T × ω
we substitute
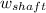 = 18 × 100
= 18 × 100
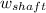 = 1800 W
= 1800 W
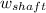 = 1.8 kW
= 1.8 kW
so
w' =
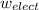 -
-
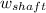
w' = 2.0 kW - 1.8 kW
w' = 0.2 kW
hence, from equation 1, dE/dt = Q' + w'
we substitute
dE/dt = -0.2[ 1 -
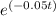 ] + 0.2
] + 0.2
dE/dt = -0.2 + 0.2
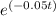 ] + 0.2
] + 0.2
dE/dt = 0.2
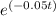
Now, the change in total energy, increment E, as a function of time;
ΔE =
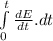
ΔE =
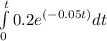
ΔE =
![\int\limits^t_0} (0.2)/(-0.05) [e^((-0.05t))]^t_0](https://img.qammunity.org/2022/formulas/engineering/college/vgke4inzvnyciv482wac9rlkeq9m5f8ewo.png)
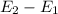 = 4[ 1 -
= 4[ 1 -
 ]
]
Therefore, the required expression is
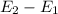 = 4[ 1 -
= 4[ 1 -
 ]
]